Fine-Tuning LLMs: LoRA or Full-Parameter? An in-depth Analysis with Llama 2
In this blog, we compare full-parameter fine-tuning with LoRA and answer questions around the strengths and weaknesses of the two techniques. We train the Llama 2 models on the same three real-world use cases as in our previous blog post. This gives us a baseline to compare task-specific performance, hardware requirements, and cost of training. We demonstrate that using LoRA involves a trade-off between serving efficiency and model quality, which varies according to the specific task at hand. Additionally, we offer insights into how to stabilize training with LoRA through intelligent prompting techniques. We further show that adopting a lower learning rate can enhance the reliability of the resulting model checkpoints. Experiments were carried out with a LoRA-adapted version of this script.
In recent months, there has been a race of open-source LLMs to compete with OpenAI’s proprietary models. One prevalent strategy for boosting the performance of open-source LLMs is full-parameter fine-tuning. In this method, all the model's parameters are optimized. We have analyzed how such full-parameter fine-tuning performs compared to prompt-engineering and few-shot prompting of GPT-4 in our previous blog post.
As you might anticipate, full-parameter fine-tuning is resource-intensive, requiring significant computational power to manage optimizer states and checkpointing. To provide some context: The optimizer states and gradients usually result in a memory footprint approximately 12 times larger than the model itself. This makes fine-tuning even the smallest Llama-2—with its 7 billion parameters—a substantial computational undertaking. Consequently, the field has seen the emergence of so-called "parameter-efficient fine-tuning" (aka peft) methods. These strategies, such as LoRA (Low-Rank Adaptation of Large Language Models), aim to refine a relatively small subset of parameters, thereby minimizing resource utilization and accelerating the training cycle.
In this blog post, we compare full-parameter to LoRA fine-tuning and highlight the pros and cons of both. Our discussion covers benchmarks on three datasets introduced from our previous blog post for which we have developed a good understanding of baselines and improvements obtained via full-parameter fine-tuning. Since LoRA is still a fairly new technique, we also discuss our experiences in training with LoRA in more detail, providing tips and tricks so that you can streamline your LoRA training experience.
We’ll be sharing more fine-tuning best practices and results at Ray Summit 2023 this Sept 18-19 in San Francisco.
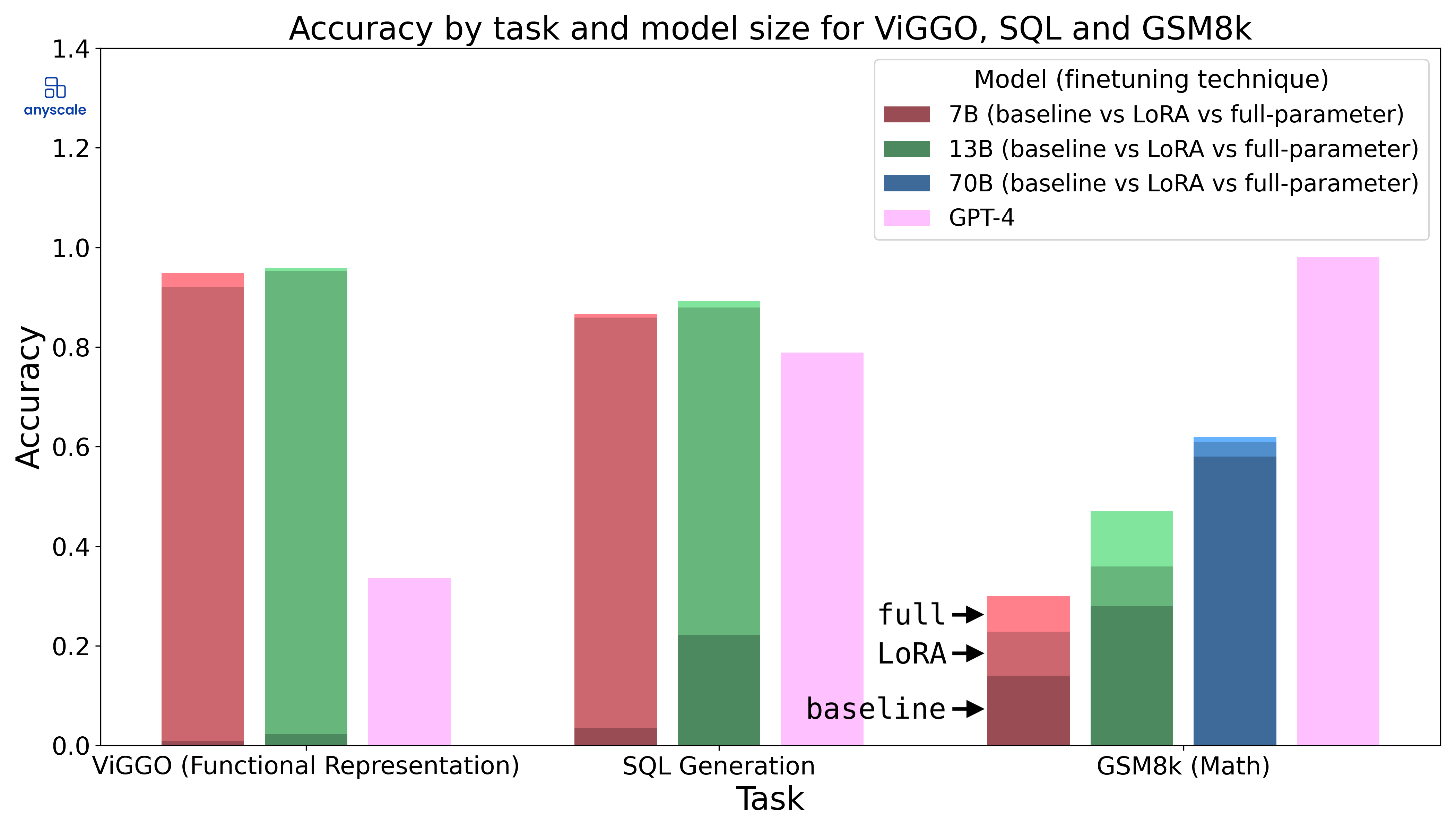
LoRA-based fine-tuning offers a performance nearly on par with full-parameter fine-tuning when applied to Llama-2 LLMs. As a result, it can outperform GPT-4 in specialized tasks like generating SQL queries or text-based functional representations, though it falls short in mathematical reasoning tasks. In the accompanying graph, the purple bars indicate GPT-4's performance; the darker bars represent the baseline chat-tuned models; the medium-shaded bars show the gains from LoRA fine-tuning; and the lightest bars display the results of full-parameter fine-tuning.
Before we compare LoRA with full-parameter fine-tuning, we briefly explain the basic concepts behind LoRA here and refer the interested reader to the original paper.
LinkWhat is LoRA?
LoRA, which stands for Low-Rank Adaptation of Large Language Models, operates on a crucial insight: the difference between the fine-tuned weights for a specialized task and the initial pre-trained weights often exhibits “low intrinsic rank” - meaning that it can be approximated well by a matrix of low rank. What does it mean for a matrix to be low rank? A low-rank matrix has few linearly independent columns, which means, in simple terms, that the matrix is less “complex”. One cool property of low-rank matrices is that they can be represented as the product of two smaller matrices. This realization leads to the hypothesis that this delta between fine-tuned weights and initial pre-trained weights can be represented as the matrix product of two much smaller matrices. By focusing on updating these two smaller matrices rather than the entire original weight matrix, computational efficiency can be substantially improved.
In practical terms, the original weight matrix remains frozen during fine-tuning. Instead, two additional matrices, A and B, are fine-tuned. These matrices act as a decomposition of the fine-tuned weight matrix. Consider the following illustration from the original LoRA paper:
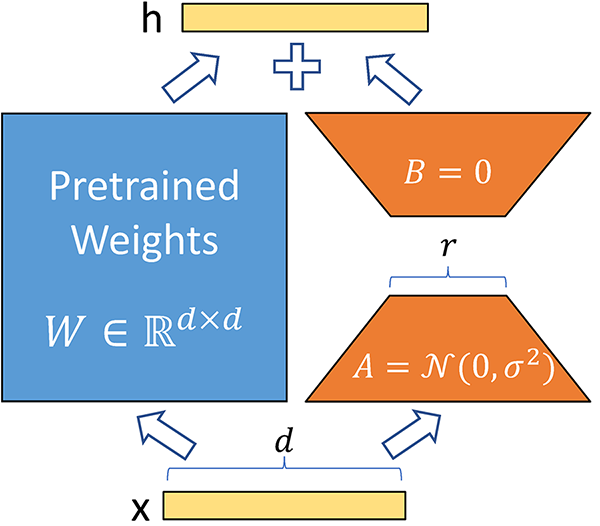
This diagram, taken from the original paper, visualizes tensor operations for one matrix within the model. A and B are the aforementioned small matrices. The input vector d is processed both through the original pre-trained weights and through LoRA's fine-tuned, low-rank decomposition matrices in parallel.
Notably, by keeping the original "Pretrained Weights" frozen during the training process and selecting r << d, both the memory footprint of the optimizer and the size of the checkpoint can be significantly reduced compared to full-parameter fine-tuning. This methodology can be applied to any dense layer within the model architecture. Since the release of the original LoRA paper, numerous techniques building upon LoRA have been introduced, though they are beyond the scope of this discussion.
The primary advantage of these parameter-efficient methods like LoRA lies in more efficient model deployment, particularly when managing multiple specialized models. This is increasingly relevant as the trend moves towards developing an array of specialized LLMs tailored for various tasks.
LinkHyperparameters
Before delving into our experimental outcomes, let's briefly cover the hyperparameters we employed as our baseline for LoRA configurations throughout this article.

The rationale behind each choice remains a subject of active debate within the Large Language Model (LLM) community, and we shed some light on our decisions below:
LinkRank: 8
Choosing a higher rank for our decomposition matrices would counteract LoRA's efficiency gains. Our preliminary tests suggested minimal performance boosts when increasing the rank to, for instance, 16. As a result, we settled on a rank of 8 to maintain smaller checkpoint sizes and to avoid artificially inflating our checkpoint files.
LinkAlpha: 16
Alpha scales the learned weights. Existing literature, including the original LoRA paper, generally advises fixing Alpha—often at 16—rather than treating it as a tunable hyperparameter.
LinkTarget modules: All dense layers
The original LoRA paper focused on fine-tuning only the "Q" and "V" attention matrices, achieving solid results that attested to the technique's efficacy. However, subsequent work has shown that targeting additional layers, or even all layers, can improve performance. We hypothesize that applying LoRA to a greater number of layers brings us closer to achieving the capabilities of full-parameter fine-tuning. Accordingly, we opted to implement LoRA across all layers.
LinkBase learning rate: 1e-4
A learning rate of 1e-4 has become the standard when fine-tuning LLMs with LoRA. Although we occasionally encountered training loss instabilities, reducing the learning rate to lower values like 3e-5 proved effective in stabilizing the process—more on this will follow.
LinkModel quality results
In a previous blog post, we demonstrated the effectiveness of fine-tuning small models for the GSM8k, ViGGO and SQL datasets. Here, we use the results obtained there as a baseline to evaluate LoRA. For more detail on the used datasets and our evaluation techniques, we refer the interested reader to that post. We will focus here on the results comparing full-parameter fine-tuning and LoRA fine-tuning.
LinkFunctional Representation of Unstructured Text (ViGGO)
The first dataset we train our models on is ViGGO. The task is to extract the functional representation from a sentence. Here is one datapoint from a failed prediction:

The data point above illustrates that this task does not require elevated levels of logic or reasoning. The task, in its essence, only requires the model to map from one representation to another. This is a task that small models with full-parameter fine-tuning can learn really well; the question is now whether LoRA can learn it as well.
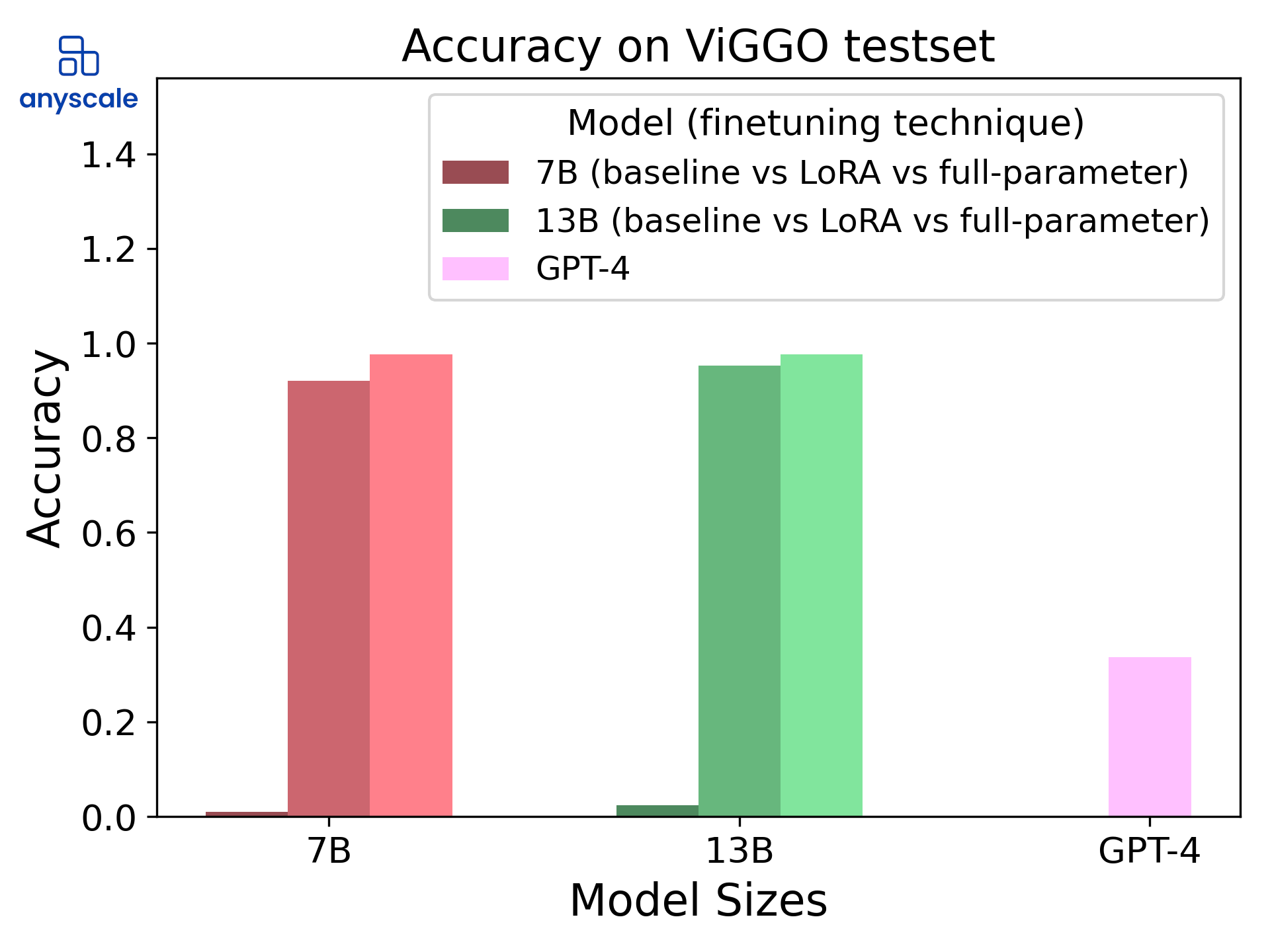
Prediction accuracy by model size and fine-tuning method on the ViGGO dataset. The plots show that our LoRA fine-tuned models are only slightly worse than the full-parameter fine-tuned models, achieving almost 100% accuracy on the ViGGO test set.
We can learn from these results that despite having done some level of hyper-parameter optimization, we have to trade off a bit of accuracy for our LoRA experiments. As a concrete example, we trade off 2% accuracy (95% vs. 97%) on the 13B models. In most real-world use cases, where we deploy the fine-tuned LLM to put it to work, LoRA would be the technique of choice because it can be served much more efficiently, and the 2% loss in accuracy may not be a big deal.
LinkGrade School Math (GSM8k)
This academic dataset tests the model’s capabilities of logic reasoning on math problems. Questions and answers are structured akin to the following:
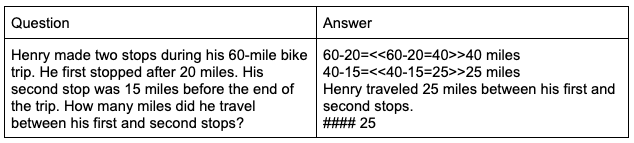
Note that there are many ways in which one could arrive at the correct answer, which stands in contrast to the other datasets we tested. With this in mind, when evaluating our models, we regard only the final answer preceded by the four hashtags. So, how well does LoRA do? The following shows the accuracy of our trained models for GSM8k:
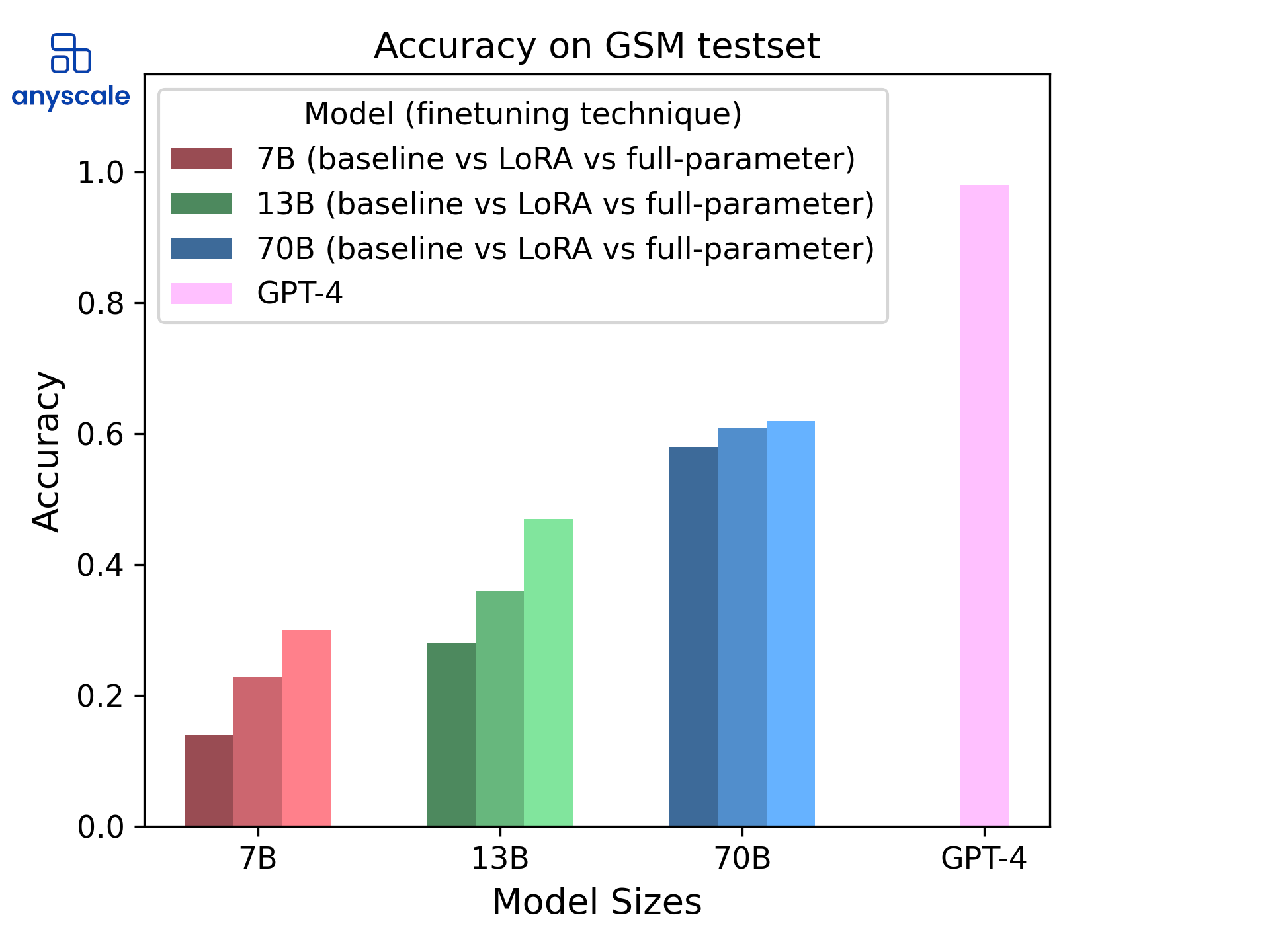
Prediction accuracy by model size and fine-tuning method on the GSM8k dataset. The two LoRA fine-tuned models underperform compared to their full-parameter fine-tuned counterparts. This is clearly not the case for the 70B model, where LoRA achieves almost the same accuracy as full-parameter fine-tuning. Having said that, the improvements on the 70B model over the baseline are relatively small.
With both fine-tuning techniques, the capacity of the base model plays a big role in the model’s aptitude for logical/mathematical reasoning. Nonetheless, LoRA consistently underperforms full-parameter fine-tuning by a significant margin. This goes back to the fact that LoRA is a low-rank approximation, one that might not best encapsulate the skill of math. Note that when compared to the other tasks, even full-parameter fine-tuning does not do particularly well. Learning math is not a trivial task – one cannot just “fine-tune” their way into developing strong mathematical reasoning abilities with only a few thousand examples.
LinkSQL
The final dataset we evaluate on is one that is connected to a real-world use case. This SQL dataset maps queries in natural language to functional SQL queries. More specifically, any data point consists of three fields:

From the similarity to the ViGGO task, we can see why a fine-tuned LLM should be a promising candidate to solve this problem. Again, the model is required to learn a set of formal principles to solve this task rather than to apply high levels of logic or reasoning.
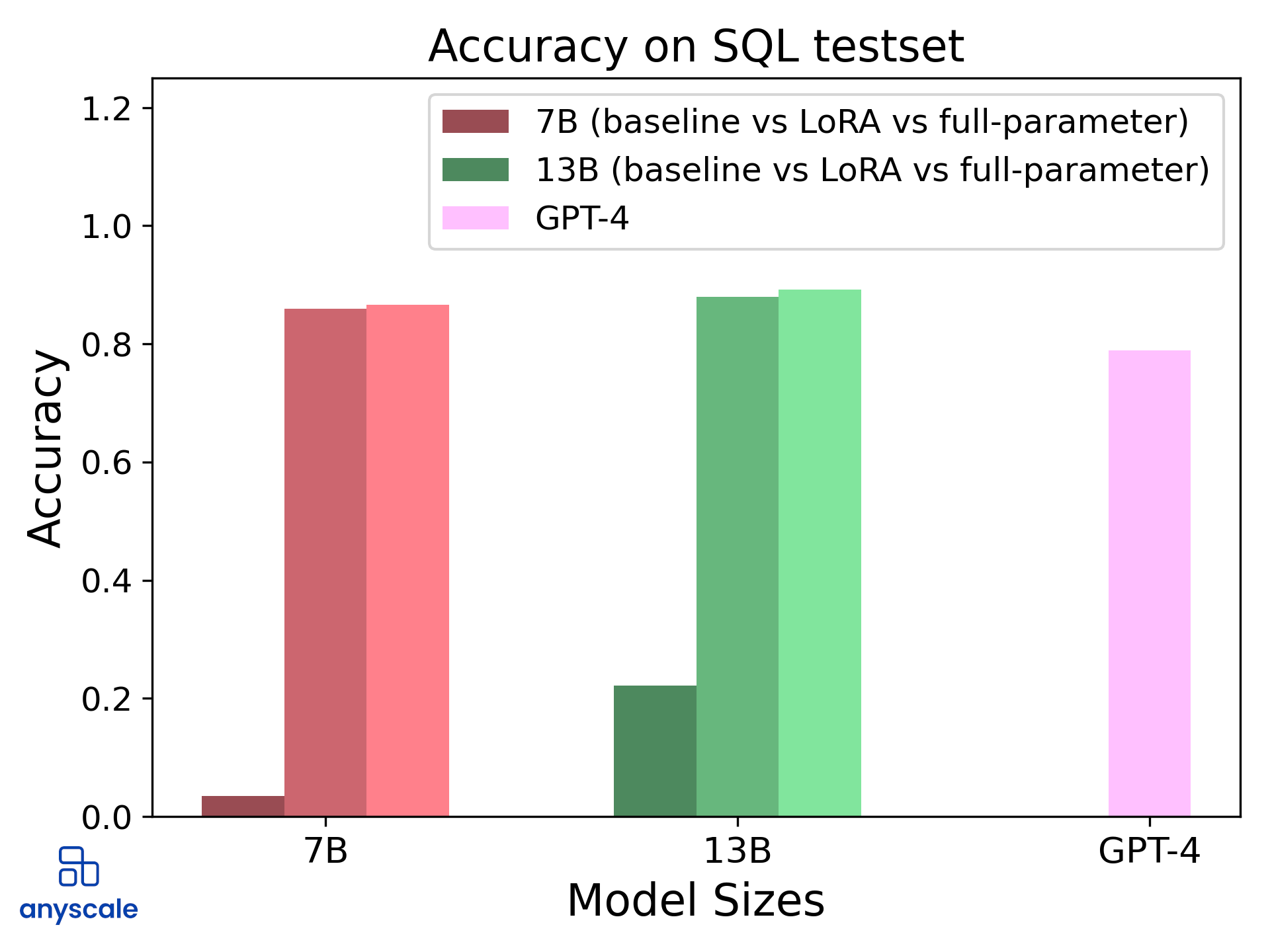
Prediction accuracy by model size and fine-tuning method on the SQL dataset. The LoRA fine-tuned models are almost on par with the full-parameter fine-tuned models. Note that the LoRA fine-tuned 13B model does slightly better than the full-parameter fine-tuned 7B model.
LinkLoRA vs Full-Parameter Fine-Tuning: Things to consider
Though LoRA is designed as an alternative to full-parameter fine-tuning, there are specific nuances to bear in mind during the training process.
LinkType of Tasks Matters
It's crucial to emphasize that LoRA serves as a low-rank approximation of the ideal weights when fine-tuning. This effectively limits the network's "adaptation capacity." To frame this mathematically, consider the original weights of the Large Language Model (LLM) as matrix "X." For any given task, the optimally fine-tuned LLM would have weights represented by matrix "Y." The objective of fine-tuning is to discover a delta matrix "Z" such that X+Z=Y. In the case of LoRA, however, this delta matrix "Z" is approximated through low-rank decomposition. Consequently, achieving an optimal solution could be challenging for certain types of tasks. Some datasets might be more readily adaptable, while others could pose difficulties. In contrast, full-parameter fine-tuning lacks this constraint; the learned weights retain the original model's expressiveness, potentially simplifying the task of fitting to diverse data. This is an empirical issue that warrants exploration through hands-on testing.
In our experiments, we observed the largest performance gap between full-parameter and LoRA fine-tuning on the GSM8k math dataset. This task required learning a challenging new skill—which might not be best captured by a low-rank approximation. For the other tasks, however, this gap was substantially narrower.
LinkSensitivity of LoRA to Learning Rate
Even for tasks where LoRA does perform well, we needed to tune the learning rate for stable training. With the limited number of parameters, the optimization landscape is trickier with LoRA than with full-parameter tuning. Consider the following graphs from the SQL experiments:
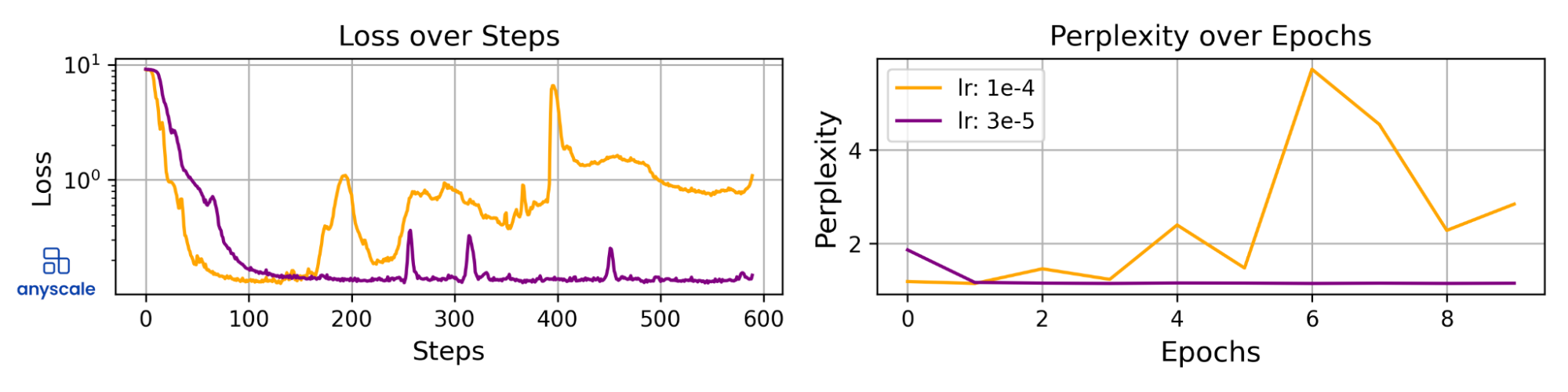
Graphs showing the impact of learning rate on the stability of the training and the perplexity on the validation set. For this specific task, we reduced the learning rate from 1e-4 to 3e-5 to stabilize the learning.
This variance in training loss understandably causes drastic differences in evaluation loss that can cause a LoRA fine-tuned model to underperform severely. While there are stability issues, when the right learning rate is chosen, convergence can be nearly optimal when measured against full-parameter fine-tuning.
Let’s set this into the perspective of fine-tuning in production. The following graph shows a fine-tuning of a 70B model with LoRA and with all hyperparameters kept constant except for the learning rate.
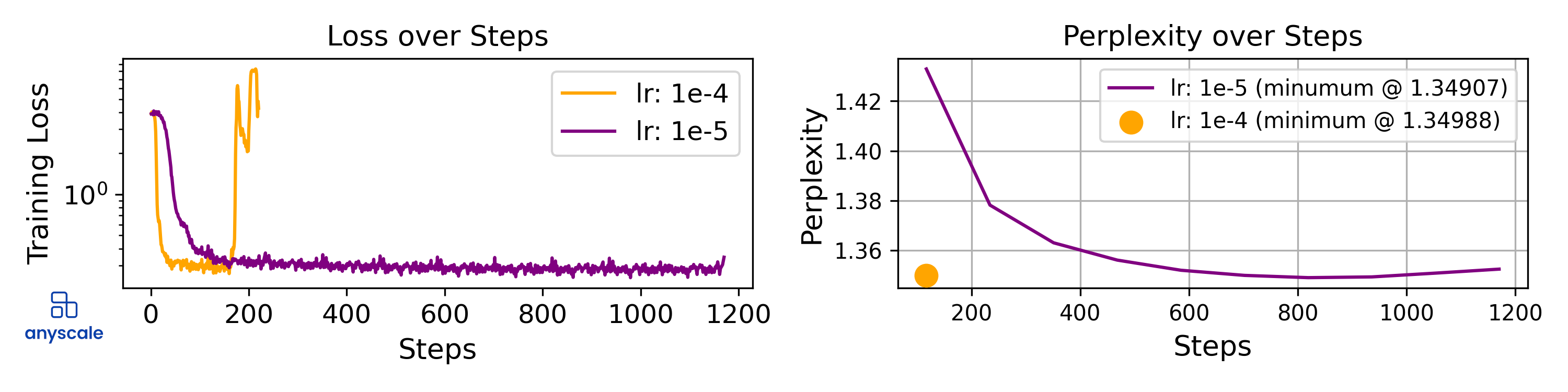
Graphs showing two trainings reaching approximately the same perplexity. For the lower learning rate, the perplexity reaches a minimum while the training loss stably decreases. For the high learning rate, the training loss explodes, leaving us with less confidence in the optimality of our checkpoint.
Both models exhibited a 61% success rate on the GSM8k dataset. While the lower learning rate produces a "textbook" learning curve, the higher learning rate appears unstable. Thus, despite the temptation to save on training costs by sticking to a learning rate of 1e-4, it's essential to recognize the potential for instability. Addressing this issue is vital for ensuring both cost-effectiveness and performance reliability in production fine-tuning.
LinkThe Role of Prompting
You might wonder, "Do I really need to engage in hyperparameter tuning?" One of the key advantages of LoRA is its efficiency in memory and serving. But if that means having to launch multiple jobs and conduct a grid-search to find the optimal configuration, it might seem less appealing. Here's where prompting can really mitigate the issue.
In our previous blog post focused on full-parameter fine-tuning, we discussed how replacing the prompt with a simple concatenation of inputs and desired outputs, separated by special learned tokens, can be effective. However, with LoRA, we found that this blind merging of inputs and outputs (even with special tokens) may not be the most stable approach. This aligns with our earlier assertion that data too far out-of-distribution can cause LoRA to struggle.
Consider the ViGGO task. In a setup without prompts, the data might appear as follows:

A properly prompted data point would include the description of the task to some extent similar to prompt engineering without few-shot examples:

Utilizing a chat format serves as a versatile framework that is applicable to a variety of tasks. The key takeaway, however, is that the description of the task would make the appearance of the tokens in the answer more likely conditioned on the tokens present in the question, making the optimization problem easier and fine-tuning more effective.
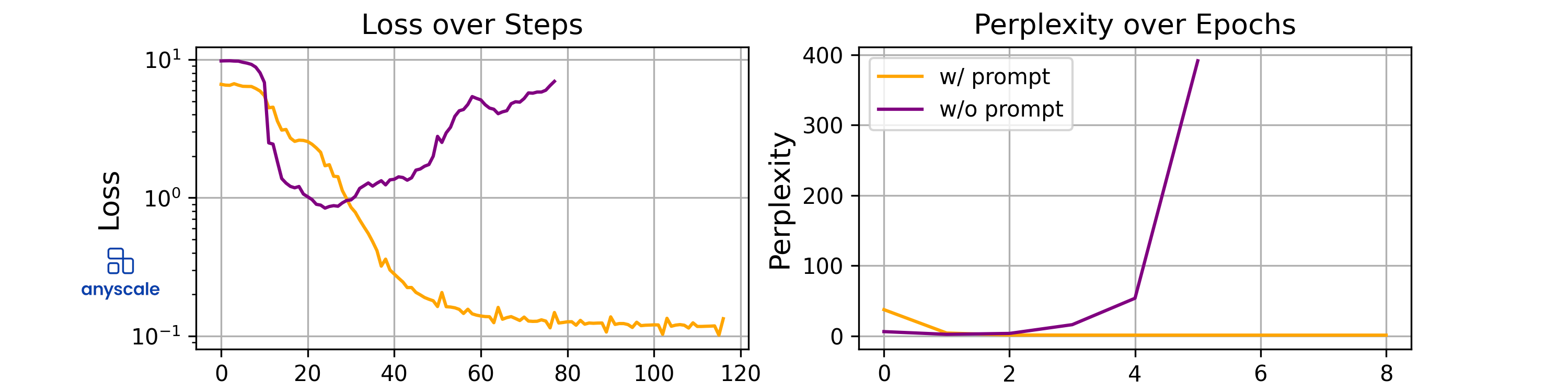
Graph showing the impact of task description prompts on model performance during fine-tuning on the ViGGO task. With other hyperparameters kept fixed, learning stability increases significantly with prompting.
While task descriptions can improve fine-tuning efficiency, they might undermine one of fine-tuning's goals—shortening the prompt. This trade-off becomes more prominent when using LoRA as your fine-tuning strategy. Therefore, you might find yourself in a cycle of experimenting with various prompts to optimize your fine-tuned model.
LinkLoRA's Interplay with Special Tokens in the Embedding Layer
As we highlighted in our previous blog post, we've integrated extra special tokens to better structure our data. These tokens bump the vocabulary size from 32,000 to 32,004 in the Llama 2 models we're working with. Naturally, this raises the question: Should we train these additional tokens? And if so, should we apply LoRA to the whole layer or make the additional embeddings trainable?
For our fine-tuning objectives, simply initializing them randomly and then applying LoRA to the whole embedding layers seems sufficient. It's crucial, however, to remember to include these randomly initialized new vocabulary embeddings in the model's checkpoint for accurate inference later on.
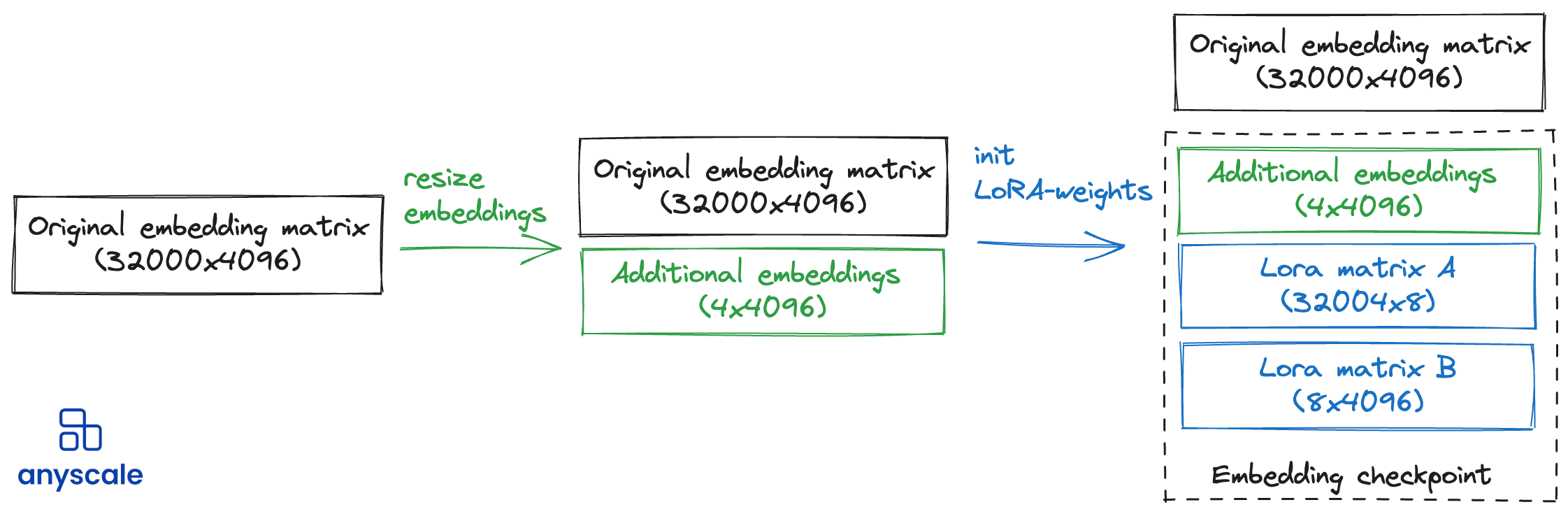
Visualization of LoRA checkpoint structure for the embedding layer. Shown here is an example for a LoRA rank of 8. In addition to the LoRA-specific matrices A and B, it's important to also save the additional embeddings that were created during the vocabulary expansion, which are initialized randomly.
LinkTraining speed benefits of LoRA
LoRA introduces new parameters and operations to the model, making the forward pass slightly slower. On the other hand, the fewer trainable parameters make the backward pass faster due to less gradient communication needed between GPUs.
We found out that without leveraging the reduced memory footprint (via increasing the batch size), LoRA doesn't offer a substantial speed advantage over full-parameter fine-tuning. That said, if your workload isn't compute-bounded, bumping up the batch size can indeed improve your training throughput.
For instance, while fine-tuning a Llama-7B model on a p4de.24xlarge node, a full-parameter approach would require a batch size of 8 to make the most out of the available GRAM memory. With LoRA, on the other hand, you can crank the batch size up to 64 and still stay within the memory constraints, thus optimizing the training speed.
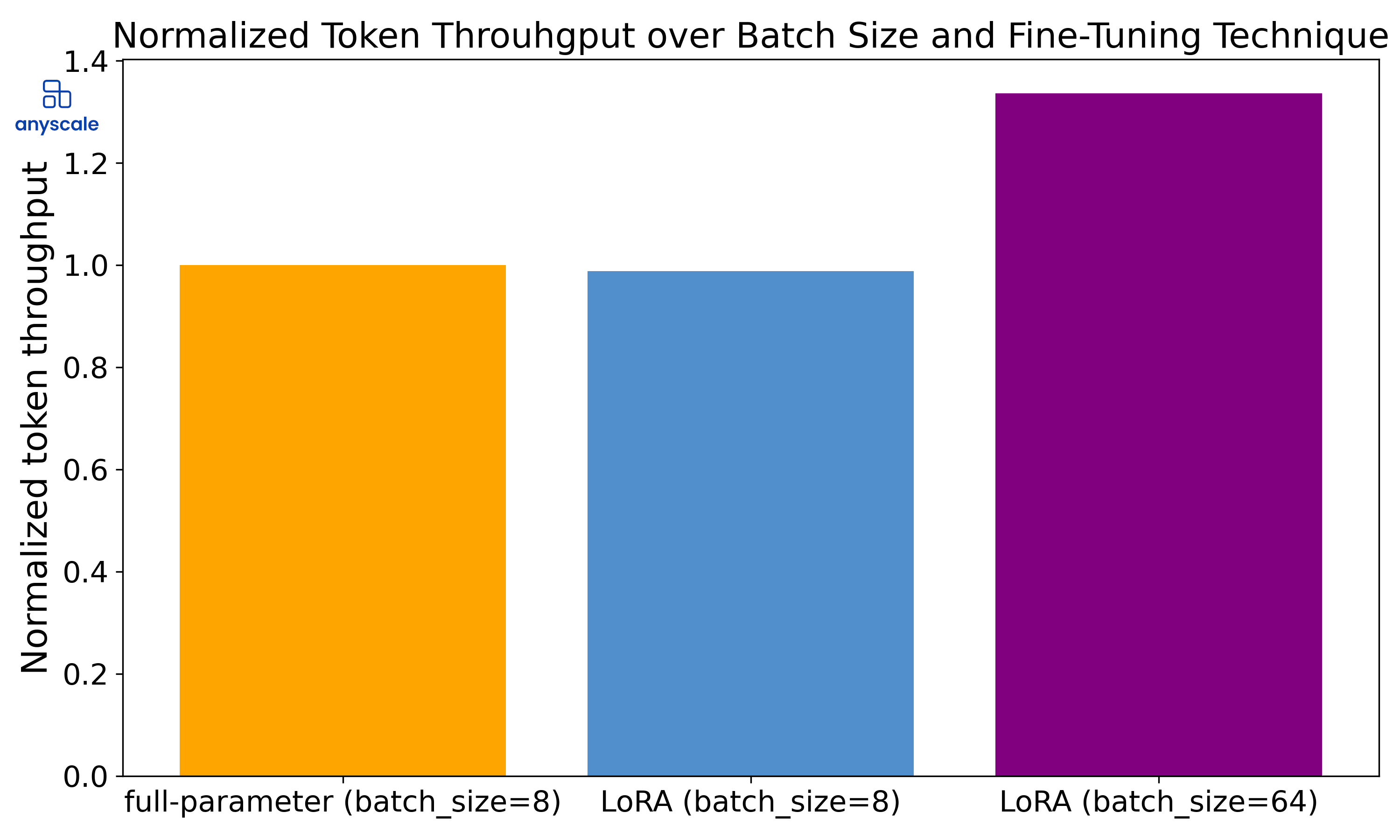
A comparison of training throughput (tokens per second) for the 7B model with a context length of 512 on a p4de.24xlarge node. The lower memory footprint of LoRA allows for substantially larger batch sizes, resulting in an approximate 30% boost in throughput.
Here's another aspect to consider: While you do witness an increase in throughput thanks to LoRA, it doesn't necessarily mean you'll reach convergence more quickly compared to full-parameter fine-tuning. LoRA, although efficient for memory, may compromise the rate at which the model converges. To illustrate this, let's look at the training loss curves from our previous experiments:
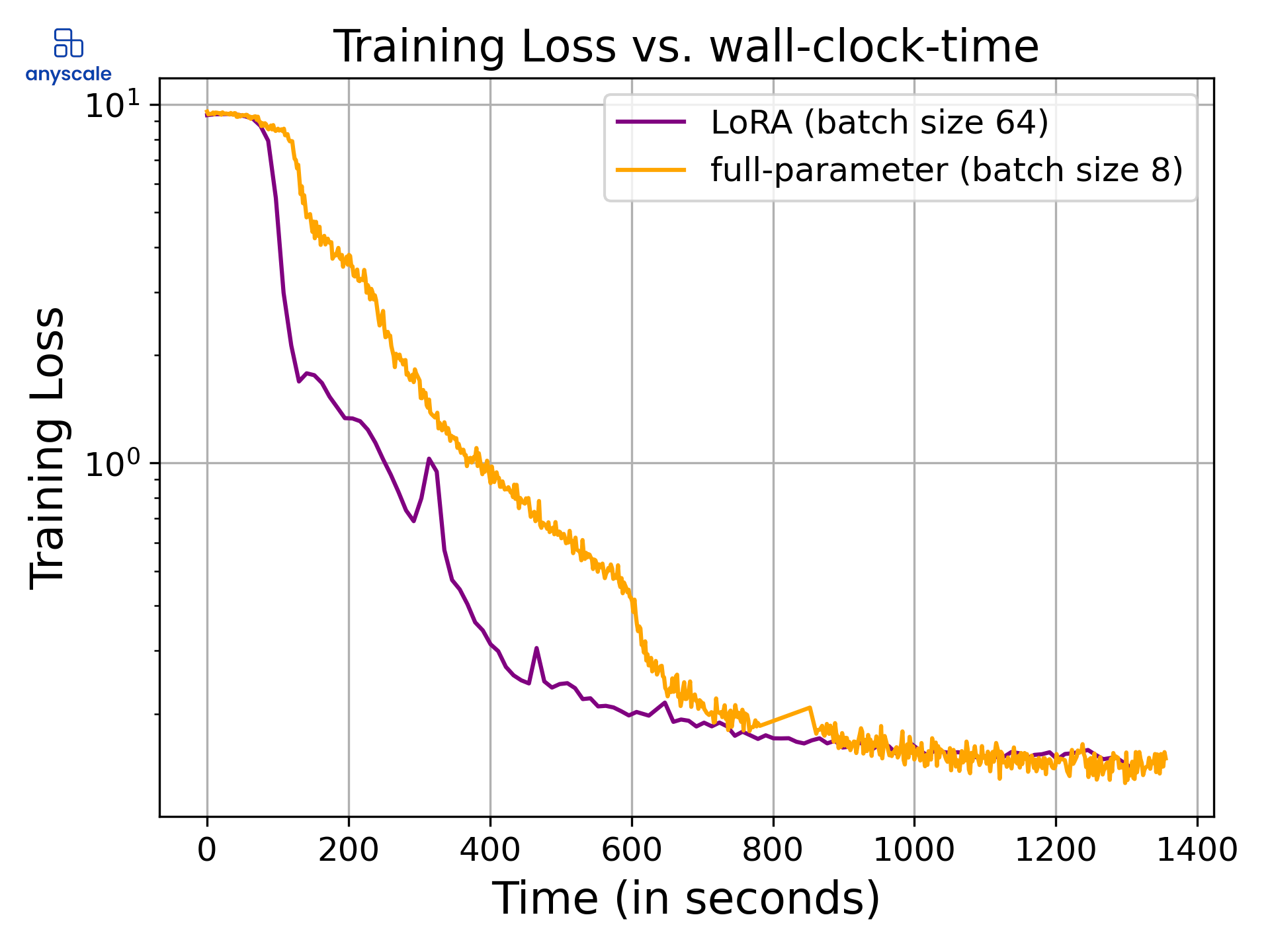
Side-by-side comparison of LoRA and full-parameter training losses, showcasing similar rates of convergence when measured in real time.
Our tests show that both methods yield comparable perplexities after a 20-minute training period. Hence, in terms of cost-effectiveness for reaching a similar-quality checkpoint, LoRA and full-parameter fine-tuning are largely on par. That said, if you're operating multiple models, LoRA's more resource-efficient deployment could be a real game-changer.
LinkMemory usage benefits of LoRA
The biggest advantage of LoRA during training is the reduced memory usage. This opens up things like the ability to fine-tune on cheaper lower-memory instances or other things like fine-tuning with a larger context length. To illustrate this, we attempted to train all model sizes (7B, 13B and 70B). Here is a side-by-side of one epoch of the memory consumption when applying full-parameter fine-tuning versus LoRA:
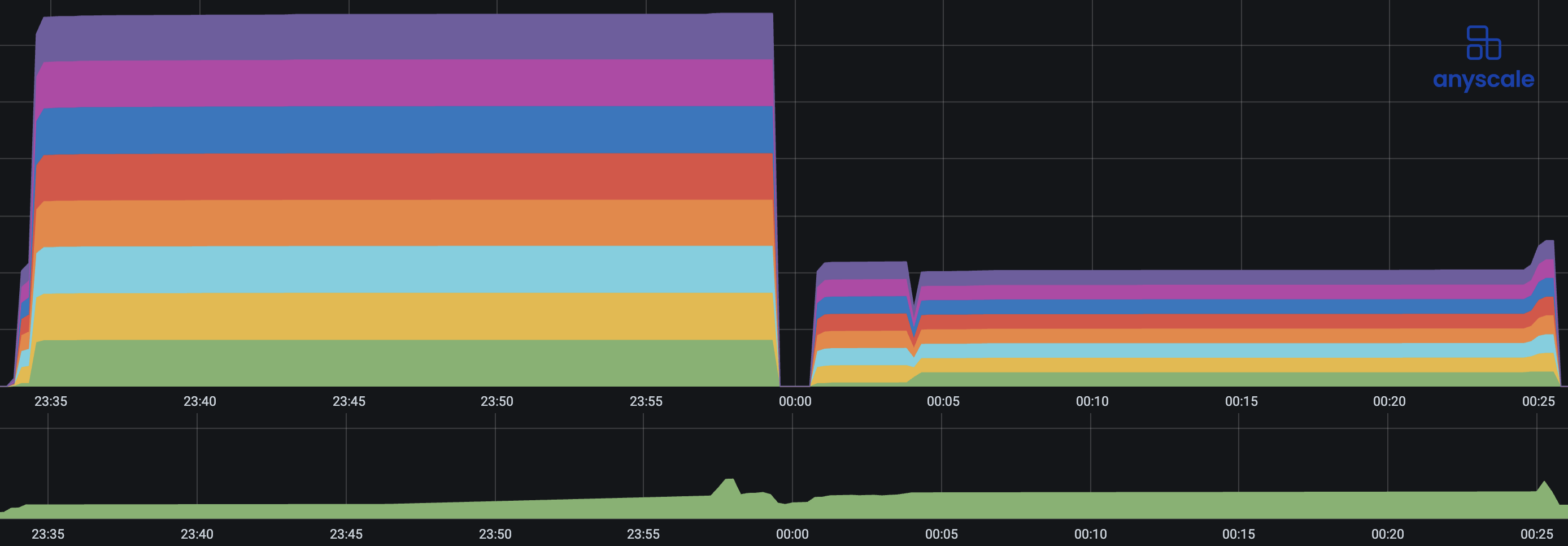
Total cluster utilization of GPU memory (top) and CPU memory (bottom) during training. The left run signifies one epoch of full-paramter fine-tuning. The right run signifies one epoch of LoRA fine-tuning. Each color on the top graph represents the memory utilization of one GPU.
We can see from these two graphs that the memory consumption peaks towards the end of an epoch—during checkpointing. We can measure the consumption of GPU memory and CPU memory during checkpointing to get an estimate of the maximum required memory. The following plot further illustrates these differences between the fine-tuning techniques:
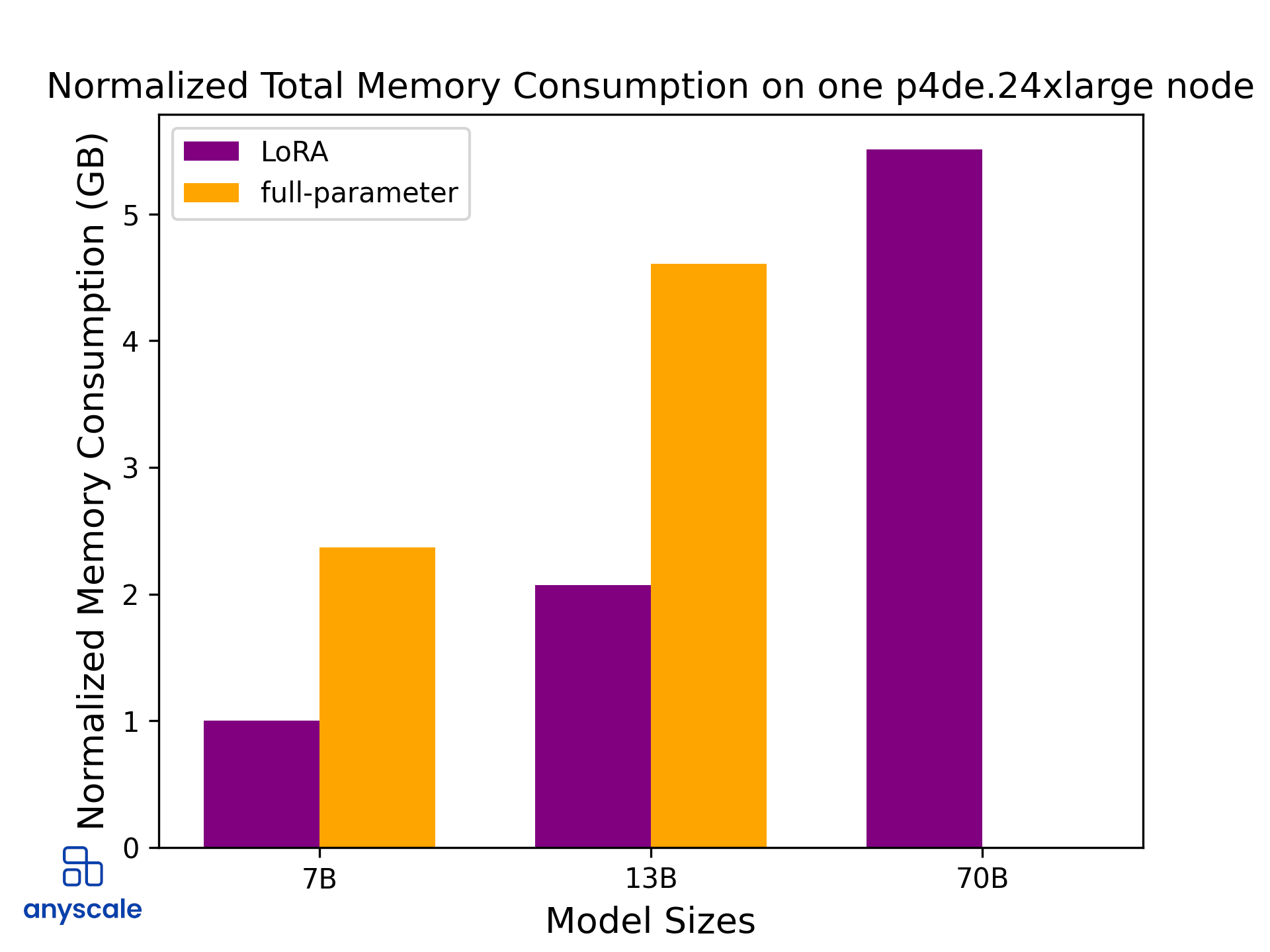
Illustration of differences in total required memory when fine-tuning the Llama 2 model series with a context length of 512 tokens and a batch size of 8 on a single p4de.24xlarge node. For the 7B and 13B models, LoRA consumes much less memory and can, therefore, be run on fewer or cheaper instances. The “missing” graph for the full-parameter fine-tuning underlines the fact that the memory requirements exceeded the specs of the p4de.24xlarge instance.
For the 70B model, we were able to run our fine-tuning jobs with LoRA on a single p4de.24xlarge node because of the smaller memory footprint. This highlights another advantage of LoRA: The significantly lower memory requirements enable us to utilize fewer resources.
LinkCheckpoint sizes and LoRA’s serving advantage
The table below delineates the difference in checkpoint sizes between full-parameter fine-tuning and two different LoRA configurations. The latter LoRA configuration, which applies LoRA to all layers, allowed us to achieve the promising accuracies detailed earlier in this post.
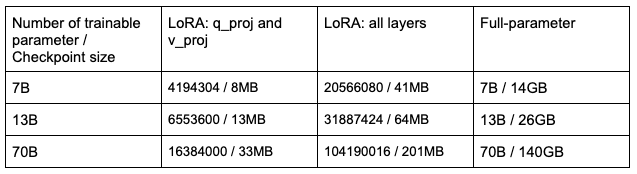
This data underscores LoRA's practical advantage for serving multiple fine-tuned models simultaneously. For context: Storing 20 fully fine-tuned 7B models would require about 280GB of space. In contrast, with our chosen LoRA parameters, that same storage could accommodate approximately 700 of our LoRA fine-tuned 70B models, the base model included.
When it comes to serving, LoRA's smaller checkpoints allow for the efficient storage and quick loading of a variety of models. This is particularly advantageous when you need a unique model for each serving request. Moreover, the ability to reuse the base model across requests in the same batch enables us to employ larger batch sizes, thus enhancing serving efficiency through increased throughput, reduced latency, and lower costs. For a more comprehensive discussion on the relationship between batch size and serving efficiency, refer to our previous blog post "How continuous batching enables 23x throughput in LLM inference while reducing p50 latency".
LinkConclusion
From our comparison of hardware requirements and prediction accuracies, we hope to have convinced the reader of the following:
The principal trade-off with LoRA is straightforward: you may give up some model quality, but you gain the ability to serve many models more efficiently.
While LoRA shines in specialized applications, it can stumble in more expansive tasks that call for, say, logical reasoning skills.
With blind concatenation of input to output, we should tune the learning rate to get reliable training checkpoints.
Don’t under-estimate the role of data prompting. It can improve training stability and enable us to choose higher learning rates without causing instability in training.
Cannot secure A100s? With LoRA you can still fine-tune models on smaller GPUs.
Compared to regular checkpoints, LoRA checkpoints are significantly smaller, facilitating more scalable serving, especially when managing multiple fine-tuned models.
LinkLearn More
We’ve demonstrated this capability and dove into a wide range of AI use cases with many of the world’s top AI pioneers from OpenAI, Netflix, Pinterest, Verizon, Instacart and others at Ray Summit 2023 in San Francisco. Both keynote sessions are available to watch if you'd like to learn more.


